Supply Chain Optimalisatie - Het is geen magie, maar wiskunde

Bedrijven met complexe toeleveringsketens moeten real-time, datagestuurde beslissingen nemen om efficiënt gebruik van middelen en eersteklas klantenservice te garanderen. Toch blijven veel organisaties vertrouwen op verouderde planningstools zoals spreadsheets en MRP. Supply chain planning op basis van wiskundige optimalisatie verschilt fundamenteel van traditionele methoden en stelt bedrijven in staat om de algehele supply chain prestaties te maximaliseren. In dit artikel wordt aan de hand van veelvoorkomende planningsscenario's uitgelegd hoe optimalisatietechnologie voor de toeleveringsketen werkt en waarom bedrijven die hun activiteiten willen stroomlijnen en hun winst willen maximaliseren, zouden moeten overwegen om over te stappen.

Optimalisatie - niet alleen voor grote bedrijven

Software voor optimalisatie van de toeleveringsketen bestaat al tientallen jaren, maar pas sinds kort is de technologie een haalbaar alternatief voor kleine en middelgrote bedrijven. Tegenwoordig kost de rekenkracht die nodig is om de optimalisatiealgoritmen uit te voeren maar een fractie van de kosten. Tegelijkertijd is de supply chain optimalisatiesoftware gebruiksvriendelijker en eenvoudiger te onderhouden geworden. Dankzij deze vooruitgang kunnen kleinere organisaties met beperkte IT-budgetten en -middelen nu profiteren van deze krachtige technologie.

Waarom heb ik optimalisatie nodig?

Optimalisatiesoftware verandert de manier waarop bedrijven hun toeleveringsketens plannen en beheren. Omdat de optimalisatiemotor rekening houdt met de beperkingen en kosten van de toeleveringsketen, worden de door het systeem gegenereerde plannen vooraf gevalideerd. De software kan de planner dus nauwkeuriger ondersteunen bij het nemen van beslissingen. Het resultaat is een betere klantenservice en een beter gebruik van de middelen met minder voorraad, wat allemaal bijdraagt aan een beter resultaat. Deze directe voordelen zijn de reden waarom optimalisatie-implementaties zo'n aantrekkelijke ROI bieden.

Hoe werkt supply chain optimalisatie?

Als mensen vertrouwen we op wat vertrouwd is en wat we begrijpen. Daarom is het essentieel voor bedrijven die vertrouwen op spreadsheets en MRP-software om de tijd te nemen om de fundamentele verschillen te begrijpen tussen traditionele planningstools en moderne oplossingen die aangedreven worden door wiskundige optimalisatie. Hoewel planners en zakelijke gebruikers de werking van wiskundige modelleer- en optimalisatietechnieken niet hoeven te begrijpen, is een goed begrip van de basis van de planningsaanpak wel nodig. Om dit inzicht te vergroten, kijken we naar de drie kernelementen van een oplossing voor optimalisatie van de toeleveringsketen:

Het Supply Chain Model (de "Digitale "Tweeling")
De Digital Twin is een elektronische weergave van uw fysieke toeleveringsketen. Het is een gedetailleerd model van uw processen en middelen, met de bijbehorende kosten en beperkingen. Het model vormt de blauwdruk voor uw planningsoplossing. Magazijnen, productielijnen, machines, voertuigen, gereedschap en personeel worden hier allemaal weergegeven.
Systeeminterfaces
De planningstool heeft accurate, actuele informatie nodig uit uw bestaande bedrijfssystemen. Afhankelijk van uw opstelling bieden directe interfaces met ERP-, PLM-, CRM- en Transportation & Warehouse Management-systemen toegang tot de benodigde invoergegevens. Voorbeelden van benodigde informatie zijn verkoopprognoses, klantorders, productinformatie en voorraadniveaus.
De oplosser
De solver is het brein van de optimalisatieoplossing en waar de magie gebeurt. Het bevat wiskundige algoritmen die samenwerken om het supply chain probleem op te lossen dat wordt beschreven door de digitale twin en de invoergegevens.
De oplosser optimaliseert een van de twee beschikbare "objectieve functies":
A. Maximale winst
B. Maximale leveringsservice tegen de laagste kosten
Als inkomsten in het model zijn opgenomen, zal de oplosser het plan bepalen dat uw totale winstgevendheid maximaliseert. Als inkomsten echter niet in het model zijn opgenomen, zal de oplosser de klantenservice maximaliseren tegen de laagst mogelijke kosten. Het is belangrijk om bewust te zijn van het verschil tussen deze twee objectieve functies. In beide gevallen zal de oplosser echter de beste algemene oplossing voor het bedrijf vinden met respect voor de gedefinieerde bedrijfsregels en beperkingen.

Optimalisatie Voorbeelden

Om een beter gevoel te krijgen voor het verschil tussen optimalisatietechnologie en traditionele planningsbenaderingen, kunnen we kijken naar enkele veelvoorkomende planningsproblemen.

VOORBEELD 1 - STANDAARD OPBOUW

Laten we beginnen met het opbouwen van een voorraad, essentieel voor bedrijven die te maken hebben met seizoensgebonden of grote promoties die pieken in de vraag veroorzaken. We hebben twee basisopties: geleidelijk de benodigde voorraad opbouwen in de loop van de tijd of extra capaciteit toevoegen dichter bij de piek. Door geleidelijk voorraden op te bouwen, kunnen we een gestage, kostenefficiënte productie handhaven en eventuele reservecapaciteit benutten. Maar het vereist ook dat we de voorraad langer vasthouden, met hogere opslag- en verwerkingskosten en een verhoogd risico op verval en veroudering. De diagrammen hieronder laten zien hoe we geleidelijk voorraden opbouwen door een gelijkmatige bezetting van de lijn (40 uur per week) in de aanloop naar de piek in de vraag in week 29 - 32 te handhaven.

Voorraadopbouw over langere periode

Het andere alternatief is het toevoegen van meer productiecapaciteit dichter bij de piek in de vraag door extra interne capaciteit toe te voegen of uit te besteden. Deze aanpak houdt de voorraadniveaus en voorraadgerelateerde kosten laag, maar de extra productiecapaciteit is meestal duur, als die al beschikbaar is.

Voorraad opbouwen met extra capaciteit dichter bij piek in vraag

De bovenstaande grafieken laten het verschil zien tussen de twee, beide potentieel levensvatbare, alternatieven. Maar welke is onze beste optie? Het zou zelfs een combinatie van de twee kunnen zijn. Als we slechts naar één geïsoleerd product kijken, is dit geen moeilijk probleem. Maar in een realistischer scenario, met honderden of zelfs duizenden producten die concurreren om productie- en distributiecapaciteit op meerdere locaties, is de optimale oplossing vaak allesbehalve voor de hand liggend, soms zelfs verrassend.

De voorraad plannen met optimalisatie

Planning gaat altijd gepaard met compromissen. Een oplossing voor optimalisatie van de toeleveringsketen bepaalt automatisch de strategie voor het aanleggen van voorraden die het best voldoet aan uw algemene bedrijfsdoelen - of het nu gaat om het maximaliseren van de totale winst of het behalen van de targets voor klantenservice tegen de laagst mogelijke kosten. Cruciaal is dat de wiskundige oplosser bij het bepalen van de voorraadstrategie rekening houdt met de hele toeleveringsketen. Als de focus alleen ligt op het voorraadproduct, zal het bedrijf als geheel daar waarschijnlijk onder lijden. Om de wiskundige optimalisatie uit te voeren, moet de oplosser toegang hebben tot de gegevens die het planningsprobleem omkaderen. In ons voorbeeld definieert het supply chain model de kosten en beperkingen met betrekking tot overwerk, kapitaalkosten, productverloop, batchgrootte, productmix en meer. En met directe toegang tot informatie over vraag en voorraden uit externe systemen, heeft de oplosser alles wat hij nodig heeft om het optimale plan te berekenen.

De voorraad plannen zonder optimalisatie

Het plannen van dezelfde voorraadopbouw met behulp van de MRP- en DRP-functionaliteit van een ERP-systeem is een heel andere uitdaging. Met tools die geen rekening houden met productie- en voorraadbeperkingen, moet de planner veel werk verzetten om de haalbaarheid van het plan te valideren. Omdat MRP en DRP geen rekening kunnen houden met planningsbeperkingen, moeten ze een reeks aannames doen, waaronder oneindige capaciteit en vaste productie- en distributietijden. Capaciteit is echter zelden onbeperkt en doorlooptijden zijn per definitie niet vast. In plaats daarvan zijn ze afhankelijk van de beschikbaarheid van materialen en de productie-, opslag- en distributiecapaciteit. Als gevolg hiervan zijn de door MRP gegenereerde plannen van veel lagere kwaliteit. Het onvermogen van MRP om een plan te leveren dat "out-of-the-box" kan worden uitgevoerd is slechts een deel van het probleem. Omdat MRP geen rekening houdt met de algehele winstgevendheid van het plan, is het moeilijk om te bepalen of het voldoet aan de bedrijfsdoelstellingen.

VOORBEELD 2 - PRoductmix

In ons tweede voorbeeld bekijken we hoe het systeem wiskundige modellering gebruikt om een planningsprobleem te optimaliseren. Het planningscenario is een bakkerij die een optimale productmix wil bepalen. Om het eenvoudig te houden, beschouwen we slechts twee producten, brood en brownies, en twee ingrediënten - bloem en suiker.

De productmix optimaliseren met optimalisatie

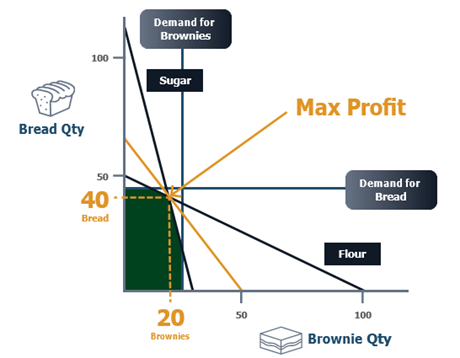
1. De meelvoorraad is beperkt tot 50 kg voor de periode. Het planningssysteem raadpleegt de product BoM's en ziet dat voor een brood 1 kg bloem nodig is en voor een brownie ½ kg. De grafiek hieronder toont de meelbeperking.

2. Na toevoeging van de aanbodbeperking voor suiker krijgen we het volgende beeld. Onze mogelijke productmix is nu gereduceerd.

3. Vervolgens worden de vraagvoorspellingen voor de twee producten, brood (45) & brownies (25), geïmporteerd uit de vraagplanner. Omdat we niet meer willen produceren dan waar vraag naar is, wordt de mogelijke productmix verder gereduceerd.

4. De optimale productmix is waar de bakkerij de maximale winst behaalt. Met een winstbijdrage van $1,50 voor brood en $2,00 voor brownies heeft het systeem alle informatie die het nodig heeft om de optimale mix te bepalen.

5. In dit voorbeeld wordt een algoritme voor lineaire programmering (LP) gebruikt om de optimale productmix te bepalen. Het systeem bepaalt de winstbijdragelijn en vindt het optimum. Denk eraan - dit gebeurt allemaal automatisch!

"Er zijn verschillende algoritmen beschikbaar, afhankelijk van de wiskundige structuur van het planningsprobleem. In dit voorbeeld kiest het systeem voor een optimalisatietechniek die Lineair Programmeren heet. Cruciaal is dat de planner geen wiskundige hoeft te zijn om het systeem te gebruiken, want dit wordt allemaal automatisch geregeld."

6. De optimale productmix is 40 broden en 20 brownies.

Het bovenstaande voorbeeld is erg eenvoudig, maar het mooie van wiskundige optimalisatie is dat we dezelfde geoptimaliseerde resultaten kunnen bereiken met duizenden producten, beperkte voorraadmaterialen en productie-, opslag- en transportmiddelen met beperkte capaciteit.

De productmix optimaliseren zonder optimalisatie

Zonder optimalisatie zal het patroon uit ons eerste voorbeeld zich herhalen. Een MRP gegenereerd plan zal de totale gevraagde hoeveelheid van 45 broden en 25 brownies produceren, ondanks de beperkte voorraad bloem. Hoewel het systeem het resulterende tekort aan bloem zal herkennen, zal dit pas achteraf duidelijk worden voor de planner. Het is dus aan de planner om het probleem op te lossen.

De rol van de planner veranderen

Werken met een MRP-systeem (zonder wiskundige optimalisatie) is heel anders dan een oplossing voor optimalisatie van de toeleveringsketen. Met MRP krijgen planners een melding als er een probleem is, maar moeten ze zelf uitzoeken hoe ze het probleem kunnen oplossen. Dit is tijdrovend en leidt steevast tot suboptimale beslissingen op basis van onderbuikgevoelens en vooroordelen in plaats van realtime gegevens en feiten. Met supply chain optimalisatie wordt planning veel proactiever en strategischer voor de organisatie. Met een systeem dat de hele toeleveringsketen modelleert en optimaliseert, hebben planners en managers een volledig overzicht van alle activiteiten en hoe ze met elkaar samenhangen. Wanneer iemand een wijziging aanbrengt in het plan, zijn de eventuele rimpeleffecten onmiddellijk zichtbaar.

Hoe optimalisatie de rol van de planner beïnvloedt

Verbeterde automatisering van de planning betekent meer tijd om te focussen op uitzonderingen.
De plannen kunnen "out-of-the-box" worden uitgevoerd met weinig of geen handmatige aanpassingen.
De planningsfunctie wordt strategischer als het vertrouwen blijft groeien.
Dankzij de snelheid van de optimalisatiealgoritmen kunnen planners meerdere what-if analyses uitvoeren voordat ze belangrijke beslissingen nemen.
De planner onderhoudt de "digitale tweeling" en houdt bedrijfsregels, kosten en beperkingen up-to-date.

Samengevat

Supply chain planning op basis van wiskundige optimalisatie kan uw bedrijf transformeren. De technologie is volwassen en heeft bewezen aanzienlijke waarde toe te voegen en is nu beschikbaar en betaalbaar voor bedrijven van alle groottes. Elke productie- of distributieorganisatie die nog geen gebruik maakt van optimalisatie van de toeleveringsketen wordt sterk aangemoedigd om uit te zoeken wat dit zou betekenen voor hun klantenservice en bedrijfsresultaat.